Tower of Hanoi


The Tower of Hanoi puzzle was invented by the French mathematician Edouard Lucas in 1883. We are given a tower of eight disks, initially stacked in increasing size on one of three pegs. The objective is to transfer the entire tower to one of the other pegs, moving only one disk at a time and never a larger one onto a smaller. However, this approach is going to examine the movement as follows:

  • Only one disk can be moved at a time.
  • A larger disk can never be placed on top of a smaller disk.

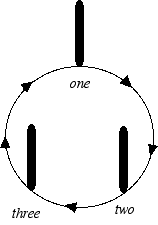
    • Further, Think of the pegs as being arranged in a circle.

     


    Demonstration Applet (Using strictly clockwise motion)

     

    Recursive solution
    Let call the three pegs Src (Source), Aux (Auxiliary) and Dst (Destination). To better understand and appreciate the following solution you should try solving the puzzle for small number of disks, say, 2,3, and, perhaps, 4. However one solves the problem, sooner or later the bottom disks will have to be moved from Src to Dst. What makes this differ from the previous approach is that all remaining disks, have to be moved to Aux. To reach Aux, they all had to be previously stacked on Dst in decreasing order. After moving the bottom disk from Src to Dst these disks will have to be moved from Aux to Dst. In order for that to occur, you have to move the disks from Aux, to Src then Dst. Therefore, for a given number N of disks, the problem appears to be solved if we know how to accomplish the following tasks:

    Move the top N-1 disks from Src to Dst (using Aux as an intermediary peg)
    Move the top N-1 disks from Dst to Aux (using Src as an intermediary peg)
    Move the bottom disks from Src to Dst
    Move the top N-1 disks from Aux to Src (using Dst as an intermediary peg)
    Move the top N-1 disks from Src to Dst (using Aux as an intermediary peg)

    This actually serves as the definition of the function for a clockwise motion. The function is recursive in that it calls itself repeatedly with decreasing values of N until a terminating condition (in our case N=0) has been met. To me the sheer simplicity of the solution is breathtaking. For N=2 it translates into

    Move from Src to Dst
    Move from Dst to Aux
    Move from Src to Dst
    Move from Aux to Src
    Move from Src to Dst

    Recurrence relations
    Let TN be the minimum number of moves needed to solve the puzzle with N disks. From the previous section T2=5 and T3=21. Now let us try to derive a general formula.

    The recursive solution above involves moving four times (N-1) disks from one peg to another and making one additional move in between. It then follows that

    TNTN-1+1+TN-1+TN-1+TN-1 = 4TN-1+1
    In other words,

    TN = 4TN-1 + 1
    Thus we can define the quantity TN as

    T1 = 1
    TN = 4TN-1 + 1 for N>1

    Thus we may compute T1 = 4T0 + 1 = 1, T2 = 4T1 + 1= 5, T3 = 4T2 + 1 = 21 and so on sequentially.

    The above expression is known as a recurrence relation which, as you might have noticed, is but a recursive function. TN is defined in terms of only one of its preceding values. This function can be made into a geometric series such that the following:
    Summation(4^n-1, as n is from 1 to n). This geometric series is not convergent, for the ratio is greater than 1. This can be made into a recursive relationship.

    Sources:
    Algebra Lab
    Cut the Knot
    Melvin Fitting